I. TRỌNG TÂM CỦA TAM GIÁC LÀ GÌ?

Ba đường trung tuyến trong tam giác đồng quy với nhau tại 1 điểm, điểm đó gọi là trọng tâm của tam giác. Trọng tâm của một tam giác cách mỗi đỉnh của tam giác ấy một khoảng bằng ⅔ độ dài đường trung tuyến đi qua đỉnh ấy.

Ví dụ: △ABC trên có 3 đường trung tuyến AN, CP, BM và chúng đồng quy tại O, O là trọng tâm △ABC.

II. TÍNH CHẤT TRỌNG TÂM CỦA TAM GIÁC

Tính chất trọng tâm của tam giác là:

• Trọng tâm của một tam giác cách mỗi đỉnh của tam giác ấy một khoảng bằng ⅔ độ dài đường trung tuyến đi qua đỉnh ấy.
• Trong tam giác, tổng các vecto đoạn thẳng từ trọng tâm đến 3 đỉnh bằng 0.

Ví dụ: △ABC trên có O là trọng tâm △ABC

• AO = ⅔ AN, CO = ⅔ CP, BO = ⅔ BM.
• (overrightarrow{OA} + overrightarrow{OB} + overrightarrow{OC} = overrightarrow{0})

III. CÁCH XÁC ĐỊNH TRỌNG TÂM CỦA TAM GIÁC

Để xác định được trọng tâm trong tam giác ta có hai cách: Xét △ABC cần tìm trọng tâm:

Cách 1:

Bước 1: Xác định điểm N là trung điểm của cạnh BC sao cho NC = NB.

Bước 2: Nối điểm A với điểm N ta được đường trung tuyến AN.

Bước 3: Tương tự đối với các đường trung tuyến còn lại.

Bước 4: Không nhất thiết phải vẽ đủ 3 đường trung tuyến mà chỉ cần dựng hai đường trung tuyến là có thể xác định được trọng tâm của tam giác, giao 2 đường trung tuyến là điểm O ⇒ O là trọng tâm △ABC.

Cách 2:

Bước 1: Xác định điểm N là trung điểm của cạnh BC sao cho NC = NB.

Bước 2: Nối điểm A với điểm N ta được đường trung tuyến AN.

Bước 3: Trên đoạn thẳng AN lấy điểm O sao cho: AO = ⅔ AN.

Bước 4: Theo tính chất trọng tâm ta xác định được O là trọng tâm △ABC.

IV. BÀI TẬP MINH HỌA VỀ TRỰC TÂM CỦA TAM GIÁC

Ví dụ: Cho △ABC, trung tuyến BM = CN, BM cắt CN tại G. Chứng minh △ABC cân tại A.

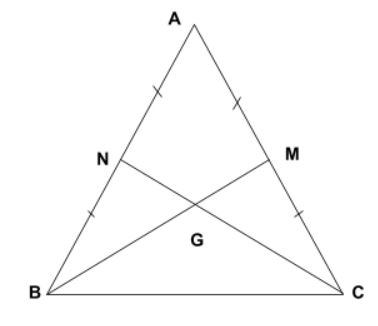
Lời giải tham khảo:

Vì BM và CN là hai đường trung tuyến của △ABC mà BM ∩ CN = {G}, nên ta có:

Mà BM = CN(gt) ⇒ BG = CG và GN = GM.

Xét △BGN và △CGM có:

(left{begin{matrix} ∠BGN = ∠CGM \ BG = CG(cmt)\ GN = GM (cmt) end{matrix}right.)

⇒ △BGN = △CGM (cgc)

⇒ BN = CM.

AB = AN + NB; AC = AN +MC mà BN = CM; M, N là trung điểm của AB, AC.

⇒ AB = AC.

Xét △ABC có AB = AC (cmt)

⇒ △ABC cân tại A. (đpcm)