Phương sai là gì? Công thức tính phương sai, cách tính phương sai và độ lệch chuẩn…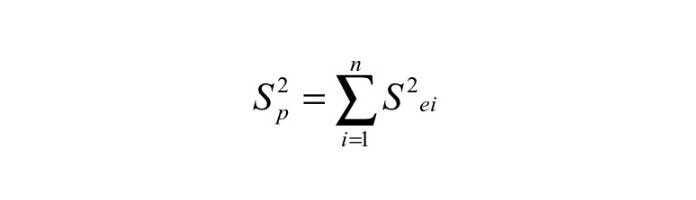

Công thức tính phương sai

Phương sai của một bảng số liệu là số đặc trưng cho độ phân tán của các số liệu so với số trung bình của nó. Phương sai của bảng thống kê dấu hiệu , kí hiệu là . Công thức tính phương sai như sau:

a) Đối với bảng phân bố rời rạc

trong đó là số trung bình của bảng số liệu.

b) Đối với phân bố tần số ghép lớp.

trong đó là giá trị trung tâm của lớp thứ .

là số trung bình của bảng.

Công thức tính độ lệch chuẩn

Căn bậc hai của phương sai một bảng số liệu gọi là độ lệch chuẩn của bảng đó. Độ lệch chuẩn của dấu hiệu , kí hiêu là .

Ghi chú: các công thức về phương sai có thể viết gọn nhờ kí hiệu như sau:

Ví dụ cách tính phương sai và độ lệch chuẩn

Ví dụ: Cho 2 nhóm có bảng số liệu như sau. Tính phương sai và độ lệch chuẩn của 2 nhóm:

Nhóm 1	Nhóm 2
160	142
160	150
167	187
156	180
161	145
= 160.8 (Mean)	= 160.8 (Mean)

Nhìn vào bảng số liệu dựa vào giá trị trung bình ta không thể đưa ra được sự phân tán bộ dữ liệu của 2 nhóm. Để xác định độ phân tán dữ liệu cần xác định độ lệch chuẩn.

Tính phương sai nhóm 1:

Nhóm 1
x
160	-0.8	0.64
160	-0.8	0.64
167	6.2	38.44
156	-4.8	23.04
161	0.2	0.04
= 160.8

Phương sai của nhóm 1:

Tính phương sai nhóm 2:

Nhóm 2
x
142	18.8	353.44
150	10.8	116.64
187	-26.2	686.44
180	-19.2	368.64
145	15.8	249.64
= 160.8

Phương sai của nhóm 2:

Bước 3: Tính độ lệch chuẩn của 2 nhóm

Độ lệch chuẩn của nhóm 1:

Độ lệch chuẩn của nhóm 2:

Như vậy độ lệch chuẩn của nhóm 1 là 3.96, độ lệch chuẩn của nhóm 2 là 21.06. Như vậy những người ở nhóm 2 có sự khác biệt nhiều hơn ở nhóm 1. Những người trong nhóm 2 nằm cách xa hơn giá trị trung bình của những người trong nhóm 1.
Sotayhoctap chúc các bạn học tốt!