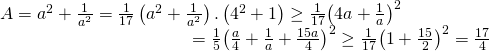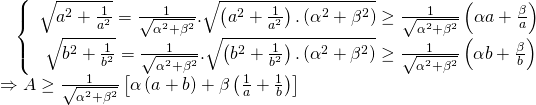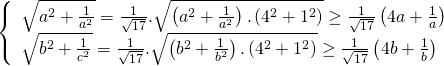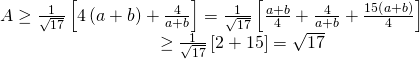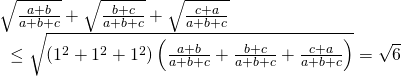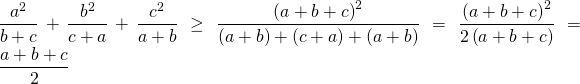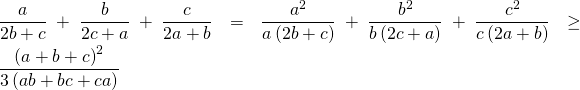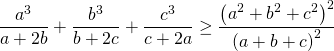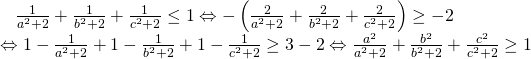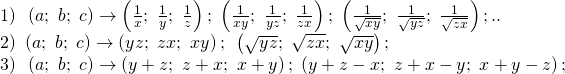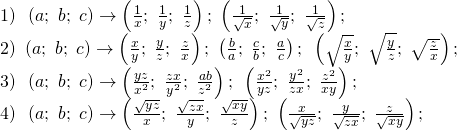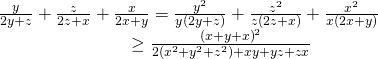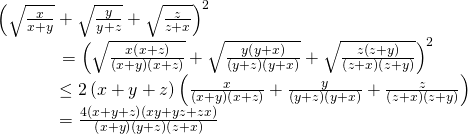Bài viết bất đẳng thức bunhiacopxki gồm có: chứng minh bất đẳng thức bunhiacopxki, bất đẳng thức bunhiacopxki và ứng dụng, bất đẳng thức bunhiacopxki mở rộng và các chuyên đề bất đẳng thức bunhiacopxki…

Bất đẳng thức bunhiacopxki

Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, do ba nhà toán học độc lập phát hiện và đề xuất, có nhiều ứng dụng trong các lĩnh vực toán học. Thường được gọi theo tên nhà Toán học người Nga Bunhiacopxki.

Cho hai dãy số thực và Ta có:

Các hệ quả của bất đẳng thức Bunhiacopxki

Hệ quả 1:

Nếu:

Thì:

Đạt được khi:

Hệ quả 2:
Nếu:

Thì:

đạt được khi:

Dấu “=” sảy ra khi và chỉ khi:

Các dạng biểu diễn của bất đẳng thức Bunhiacopxki

Dạng tổng quát

+ Cho hai dãy số tùy ý và . Khi đó ta có:

Dạng 1:

Dạng 2:

– Dấu đẳng thức xảy ra ở dạng 1 và dạng 2 là:

Dạng 3:

– Dấu đẳng thức xảy ra ở dạng 3 là:

Dạng 4: Cho hai dãy số tùy ý và với

Khi đó ta có

– Dấu đẳng thức xảy ra ở dạng 4 là:

Trong các dạng trên thì bất đẳng thức dạng 1, dạng 2, dạng 3 gọi là các bất đẳng thức Bunhiacopxki dạng cơ bản và bất đẳng thức dạng 4 còn được gọi là bất đẳng thức Bunhiacopxki dạng phân thức.

Một số dạng đặc biệt

Một số kỹ thuật sử dụng bất đẳng thức Bunhiacopxki

Kỹ thuật chọn điểm rơi

Cũng tương tự như bất đẳng thức Cauchy, khi sử dụng bất đẳng thức Bunhiacopxki để chứng minh bất đẳng thức ta cần phải bảo toàn được dấu đẳng thức xẩy ra, điều này có nghĩa là ta cần phải xác định được điểm rơi của bài toán khi áp dụng bất đẳng thức Bunhiacopxki. Để rõ hơn ta tìm hiểu một số ví dụ sau:

Ví dụ 1.1: Cho a là số thức dương thỏa mãn mãn . Tìm giá trị nhỏ nhất của biểu thức:

+ Sai lầm thường gặp:

Sai lầm 1: .

Sai lầm 2:

Do đó giá trị nhỏ nhất của A là .

+ Nguyên nhân sai lầm: Để có giá trị nhỏ nhất là thì dấu đẳng thức xẩy ra tại

trái với giả thiết

+ Phân tích tìm lời giải: Xét bất đẳng thức với dấu đẳng thức xẩy ra tại . Giả sử với các số ta có

Ta cần chọn hai số sao cho giá trị nhỏ nhất của A đạt được tại . Từ đó ta có sơ đồ điểm rơi:

+ Lời giải đúng: Áp dụng bất đẳng thức Bunhiacopxki ta có

Vậy giá trị nhỏ nhất của A là . Đẳng thức xẩy ra khi và chỉ khi .

Ví dụ 1.2: Cho a, b, là các số thực dương thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức:

+ Sai lầm thường gặp:

Do đó giá trị nhỏ nhất của A là .

+ Nguyên nhân sai lầm: Để có giá trị nhỏ nhất là thì dấu đẳng thức xẩy ra tại

Khi đó trái với giả thiết

+ Phân tích tìm lời giải: Xét bất đẳng thức với dấu đẳng thức xẩy ra tại . Khi đó với ý tưởng chuyển đổi một biểu thức trong căn thành một biểu thức ngoài căn. Giả sử với các số ta có

Do A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt được tại . Từ đó ta có sơ đồ điểm rơi:

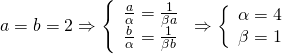
+ Lời giải đúng: Áp dụng bất đẳng thức Bunhiacopxki ta có

Khi đó ta được

Để ý ta thấy , do đó áp dụng bất đẳng thức Cauchy và giả thiết ta được

Dấu đẳng thức xẩy ra

Vậy giá trị nhỏ nhất của A là . Đẳng thức xẩy ra khi .

Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng cơ bản

Bất đẳng thức Bunhiacopxki dạng cơ bản là những bất đẳng thức đánh giá từ đại lượng về đại lượng hoặc ngược lại. Để rõ hơn ta xét một số ví dụ sau:

Ví dụ 2.1: Cho a, b, c là các số thực dương thỏa mãn . Chứng minh rằng:

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki ta được

Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi .

Ví dụ 2.2: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki ta được

Do đó ta được

Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi

Ví dụ 2.3: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:

Phân tích: Để ý là . Do đó ta nghĩ đến việc đưa hai đại lượng dưới dấu căn vào trong cùng một dấu căn. Chú ý đến chiều của bất đẳng thức ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng cơ bản

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki cơ bản dạng

, ta được

Do đó ta được

, tương tự ta có

Cộng theo vế các bất đẳng thức trên ta được

Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại .

Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng phân thức

Bất đẳng thức Bunhiacopxki dạng phân thức là bất đẳng thức có ứng dụng rộng rãi trong chứng minh các bài toán bất đẳng thức. Nó giải quyết được một lớp các bất đẳng thức chứa các đại lượng có dạng phân thức.

Ví dụ 3.1: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

Phân tích: Quan sát các đại lượng bên vế trái và chiều bất đẳng thức, một cách tự nhiên ta nghĩ đến bất đẳng thức Bunhiacopxki dạng phân thức

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi

Ví dụ 3.2: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

Phân tích: Quan sát các đại lượng bên vế trái và chiều bất đẳng thức, một cách tự nhiên ta nghĩ đến bất đẳng thức Bunhiacopxki dạng phân thức

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi

Nhận xét: Nếu ta thay các biến a, b, c tương ứng bởi thì ta thu được bất đẳng thức

Để ý ta lại thấy , khi đó ta được bất đẳng thức

Ví dụ 3.3: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

Phân tích: Quan sát vế trái của bất đẳng thức cần chứng minh ta cũng có thể nghĩ đến việc vận dụng bất đẳng thức Bunhiacopxki dạng phân thức. Nhưng nếu để như thế mà áp dụng thì không được. Trước hết ta cần tạo ra các biểu thức có dạng bình phương ở tử có 3 phân thức ở vế trái bằng cách nhân thêm vào tử và mẫu các lượng thích hợp.

Để ý là

.

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

Tuy nhiên đánh giá trên ta một đánh giá đúng.

Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi khi và chỉ khi

Ví dụ 3.4: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Ta lại có

Do đó ta được

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi

Kỹ thuật thêm bớt

Có những bất đẳng thức (hay biểu thức cần tìm GTLN, GTNN) nếu để nguyên dạng như đề bài cho đôi khi khó hoặc thậm chí không thể giải quyết bằng cách áp dụng bất đẳng thức Bunhiacopxki. Khi đó ta chịu khó biến đổi một số biểu thức bằng cách thêm bớt các số hay biểu thức phù hợp ta có thể vận dụng bất đẳng thức Bunhiacopxki một cách dễ dàng hơn. Ta cùng xem xét các ví dụ sau để minh họa cho điều đó.

Ví dụ 4.1: Cho a, b, c là các số dương thỏa mãn . Chứng minh rằng:

Phân tích: Các đại lượng vế trái của bất đẳng thức cần chứng minh có dạng phân thức nên suy nghĩ đầu tiên là sử dụng bất đẳng thức Bunhiacopxki dạng phân thức. Nếu áp dụng bất đẳng thức Bunhiacopxki dạng phân thức một cách trực tiếp ta thu được bất đẳng thức

Để hoàn thành phép chứng minh ta cần đánh giá được . Tuy nhiên để ý là đại lượng trội nhất nên không thể đánh giá về đại lượng trội hơn

Do đó ta không thể áp dụng trực tiếp bất đẳng thức Bunhiacopxki để chứng minh được, vì vậy ta tính đến phương án đổi chiều bất đẳng thức trước. Chú ý là

Như vậy ta có phép biến đổi tương đương bất đẳng thức như sau

Đến đây ta có thể áp dụng được bất đẳng thức Bunhiacopxki dạng phân thức để đánh giá bất đẳng thức

Lời giải

Bất đẳng thức trên tương đương với

Hay

Áp dụng bất đẳng thức bunhiacopxki dạng cộng mẫu kết hợp với giả thiết ta được

Do đó bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi .

Ví dụ 4.2: Cho a, b, c là các số thực dương. Tìm giá trị lớn nhất của biểu thức:

Phân tích: Bất đẳng thức cần chứng minh tương đương với

Đến đây ta có thể áp dụng bất đảng thức Bunhiacopxki dạng phân thức được.

Lời giải

Thật vậy, bất đẳng thức trên tương đương với

Hay

Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta được

Do đó bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi .

Ví dụ 4.3: Cho a, b, c là các số thực dương thỏa mãn . Chứng minh rằng:
x

Lời giải

Bất đẳng thức cần chứng minh tương đương với

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Ta cần chứng minh

.

Từ giả thiết của bài toán ta được và từ đánh giá quen thuộc , suy ra ta được

.

Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi .

Kỹ thuật đổi biến trong bất đẳng thức Bunhiacopxki

Có một số bất đẳng thức, nếu ta để nguyên dạng phát biểu của nó thì rất khó để phát hiện ra cách chứng minh. Tuy nhiên bằng một số phép đổi biến nho nhỏ ta có thể đưa chúng về dạng quan thuộc mà bất đẳng thức Bunhiacopxki có thể áp dụng được. Trong mục này chúng ta cùng tìm hiểu kỹ thuật đổi biến trong bất đẳng thức Bunhiacopxki.

Với bất đẳng thức ba biến a, b, c ta có thể sử dụng một số phép biến đổi như:

Với một số bất đẳng thức có giả thiết là ta có thể đổi biến

Ví dụ 5.1: Cho a, b, c là các số thực dương thỏa mãn . Chứng minh rằng:

Phân tích: Bất đẳng thức cần chứng minh được viết lại thành

Để ý ta thấy bất đẳng thức có sự lặp lai của các đại lương và chú ý ta nhận thấy . Do vậy một cách tự nhiên ta nghĩ đến phép đổi biến là .

Lời giải

Bất đẳng thức cần chứng minh tương đương với

Đặt , khi đó ta được , bất đẳng thức cần chứng minh trở thành

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

Ta cần chứng minh

Thật vậy, bất đẳng thức trên tương đương với

Đặt suy ra , khi đó ta cần chứng minh .

Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra khi .

Ví dụ 5.2: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

Phân tích: Bất đẳng thức được viết lại thành

Quan sát bất đẳng thức trên ta nghĩ đến phép đổi biến , khi đó bất đẳng thức trở thành

Đây là bất đẳng thức được chứng minh trong mục 2 với phép đối xứng hóa.

Lời giải

Đặt , khi đó bất đẳng thức cần chứng minh trở thành

Áp dụng bất đẳng thức Bunhiacopxki ta được

Ta cần chứng minh

Hay

Hay

Bất đẳng thức cuối cùng là một bất đẳng thức đúng.

Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại .
Sotayhoctap chúc các bạn học tốt!